I will try to describe precisely and with examples what "Heap" is in theory and in practice. In the introduction, we can say that the heap is a kind of data structure representing a particular type of tree. The heap is also an extremely effective implementation of an abstract type of data called priority queue. Now let us explain exactly what has been written above.
When tree becomes a heap?
For a tree to be a heap, it must meet a few conditions. I will list them and then try to explain them more clearly. Let us take a look at these two heaps:

Label: An example of Max-Heap, and Min-Heap
At first glance, we can see that Max Heap keeps the biggest element of the whole tree in his root and Min Heap keeps the smallest element of the whole tree in his root. We can also see that each node contains children who are smaller than him. This knowledge is a good start.
Heap must be a complete binary tree
So what are complete binary trees? We can say that a complete binary tree is one that has the same number of nodes at each level -- except at the last level where there does not have to be the same number of nodes but they have to be left-aligned. Sounds complicated? Believe me, it is not. Let's add some more information to this explanation and then help ourselves with the illustration. If we write down an array, reading a binary tree from left to right from the upper level to the last lower level, we should get some kind of array, which should not have any blanks. An example:
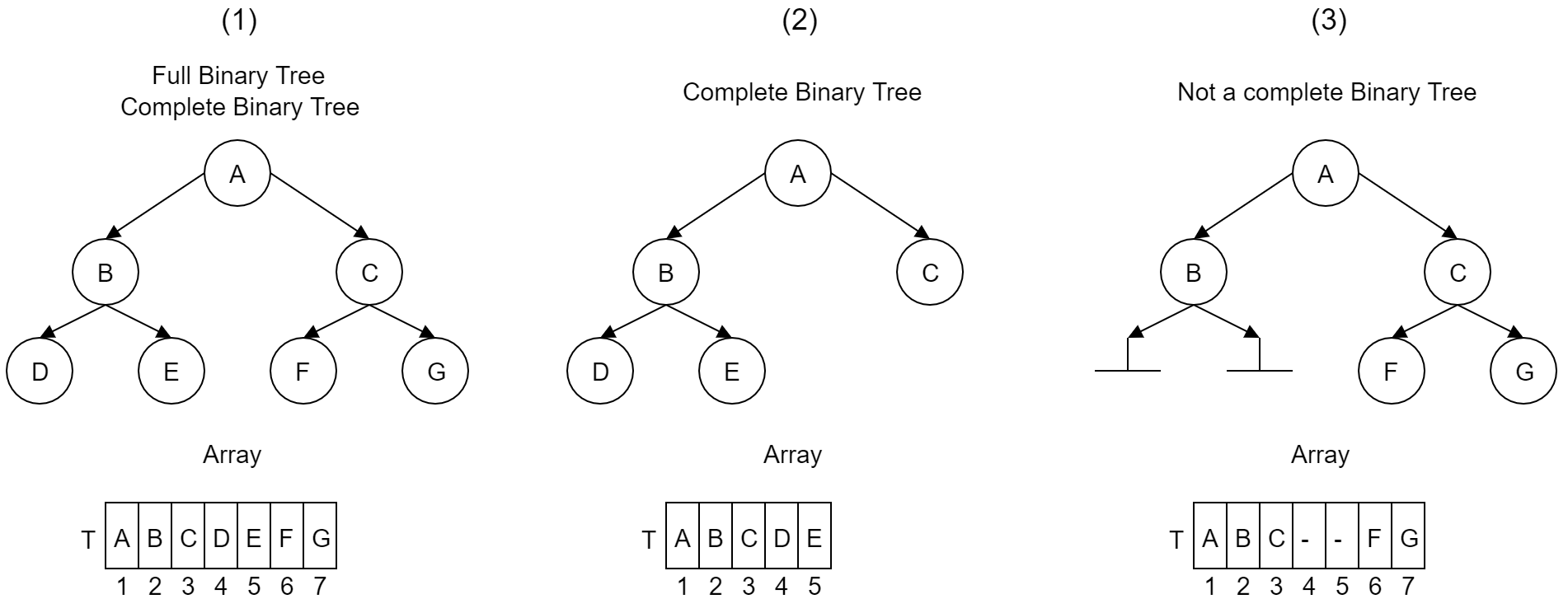
Label: An example of how to distinguish a complete binary tree
I still don't know how to get this array...
A simple matter, let us look again at a better example. Please also note the difference between max-heap and min-heap. In max-heap a parent is always bigger than his children and the biggest element in the structure is the root. In a min-heap it is in totally opposite way. To create an array, I read elements from left to right, starting with the highest level and ending with the lowest level.

Label: How to build an array from the heap?
Okay, but if I have only the array, then how should I read it?
Let us say that the node is on the i index.
Then its left child will be on index $2 \cdotp i$.
Its right child will be on index $2 \cdotp i + 1$.
Finally its parent will be on index floor($\frac{i}{2}$), where the floor of course means rounding down.
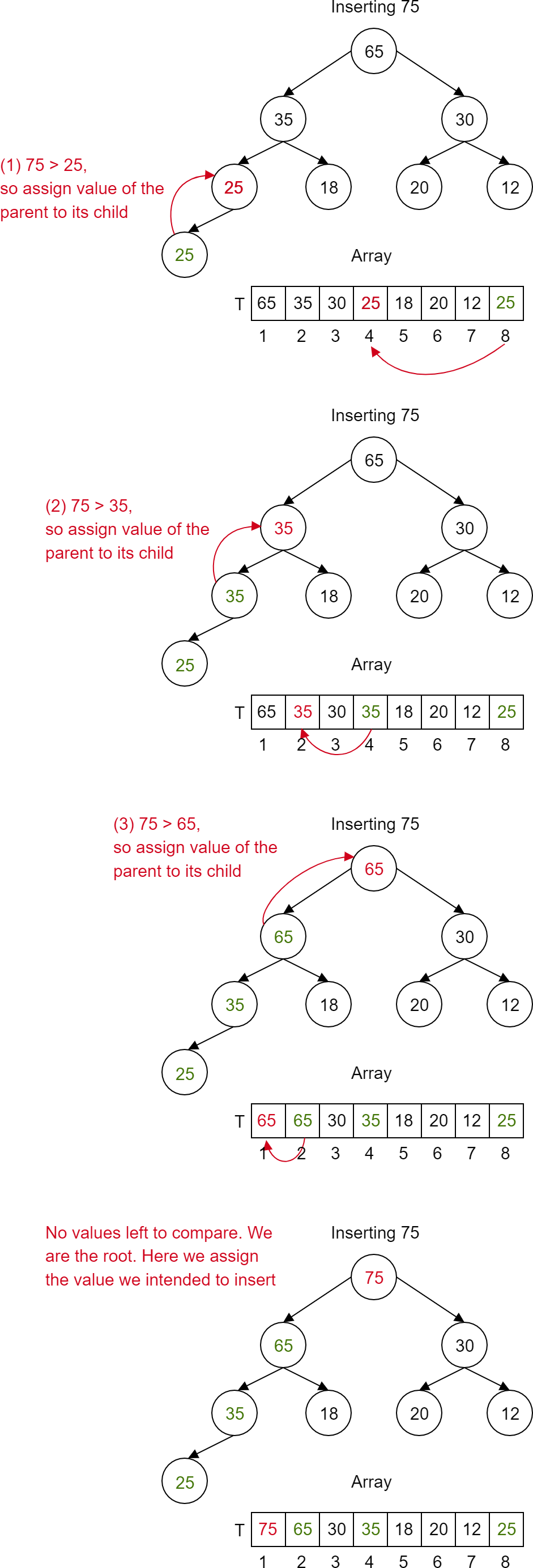
For example below, the parent of index 8 will be index 4, because $\frac{8}{2} = 2$. This means that the parent of the number 75 is 25.
| value: | 65 | 35 | 30 | 25 | 18 | 20 | 12 | 75 |
|---|---|---|---|---|---|---|---|---|
| index: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Definition
Since we already know more practically what it looks like, let us talk a little bit about theory.
Heap is a data structure that supports the following operations (max-heap in this situation).
- insert -- insert an element into the structure
- get_max -- return the largest element of the structure (get_min for min-heap)
- extract_max -- remove the largest element of the structure (extract_min for min-heap)
Sometime also decrease_key is required which decrease the value related to some (pointed directly) element of the structure (increase_key for min-heap).
The common implementation of heap is binary heap. Binary Heap is a binary tree (binary tree contains at most 2 children), although please do not confuse this with Binary Search Tree -- because ordering in BST is different. We can say that Binary Heap is some kind of subset of Binary Trees as there are several properties that the Binary Tree must fulfil here to become a Binary Heap. The most important one are:
- heap ordering -- node must be larger than both of its children
- heap shape -- in heap of height h all levels up to h - 1 are completely filled but at the h-th level (in other words last bottom level) the nodes are left-aligned.
Now let us move to the operations on the heap.
Get maximum/minimum
Implementation of this is very simple. As maximum is stored as the root for max-heap, and minimum is stored as the root for min-heap we can easily get those values by accessing first index of the array -- A[0], or A[1] if someone prefers to start from 1 (or if you are into R language). Thus time complexity is simply constant <b>O(1)</b>.
Insertion
If we want to add a new element to the heap, we add it as a new leaf at the end of the array.

We then compare the newly added object with its parents. If the current parent is smaller than him (in case of max-heap), we swap those two nodes.

This operation of moving node towards the root is called a <b>sift-up</b>. It is used to restore heap condition after insertion. Going toward the root of the heap we won't visit more than h nodes, and at each level we compare just two elements. Thus we know that time complexity is proportional to the height of the tree and assuming that our heap is implemented as Binary Heap, which is Balanced Binary Tree -- where height is log(n) then our time complexity is <b>O(log n)</b>.
I would like to mention one thing here. As this is more of an article for dummies I thought it would be easier to think about it as swapping nodes. But in fact the nodes are not swapped, only the value of the "swapped" parent are assigned to the child until we reach a situation where we can't travel any further up the tree so we assign the value that we want to insert to the node we stopped at. Swapping elements so many times would be an expensive operation, but it is easier to think about nodes that they are "swapped".
Referring to the tip above. If we wanted to speed up the process instead of "swapping" we could always just remember the value we are inserting and only assign it when we are at the position where we should do so. Alternatively then this example at the top would look a little different. Please note that the "child" mentioned here is the current position in the heap we are on.
Label: The same "insertion" operation, but without swapping.
Deletion
The only thing we can remove is the root. Why is that? We can imagine it as a huge pile of cans from which we can only take the can on top... unless we want everything to fall down. Remove the root and then insert the last element from the array in its place. Of course, the tree obtained is unlikely to be a heap yet. For this purpose, we compare the children of the new root with the larger child. If this child is larger then we swap those two nodes. We repeat the operation as long as the children of the node are smaller than it, or as long as the node no longer has any children.
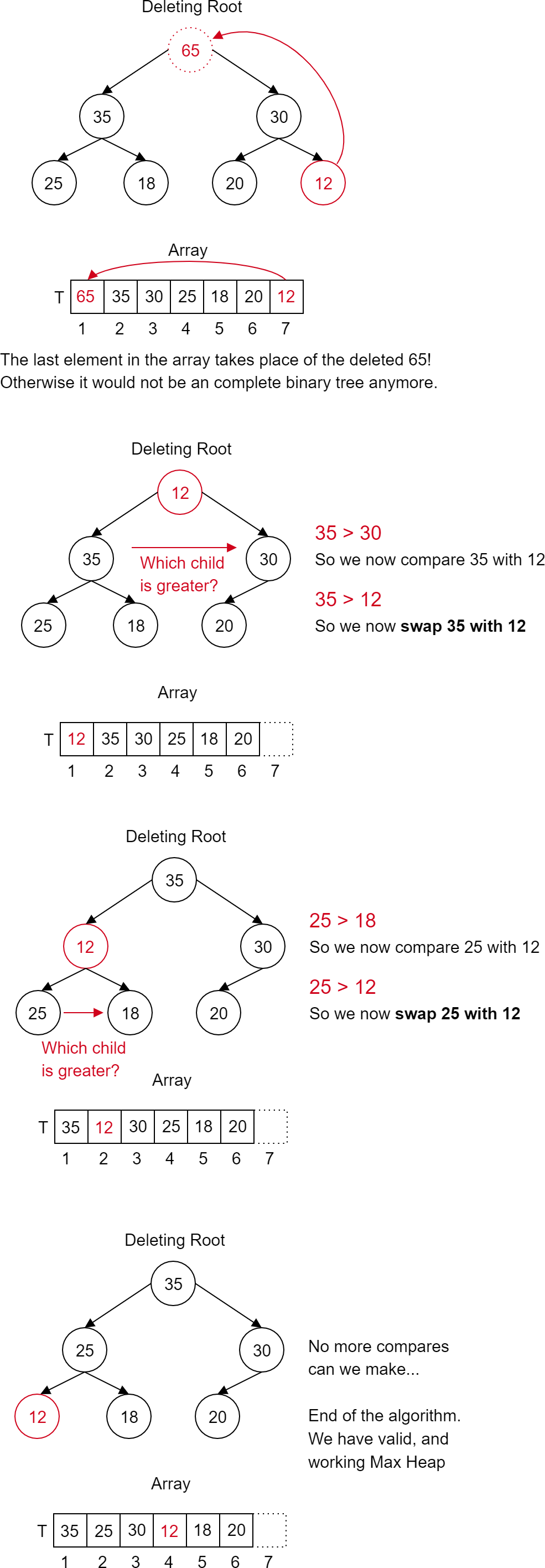
This operation of moving node down towards the leaves is called a <b>sift-down</b>. It is used to restore heap condition after deletion.
In summary:
- We remove the root node
- In its place we insert the last element of the array (at h-th / last level the most right-aligned leaf)
- Then we fix the heap by performing sift-down which compares the "bad node" with its larger child till it will be larger than its two children.
Time complexity again like it was in Insertion is proportional to the height of the Binary Heap (log(n)), thus time complexity is <b>O(log n)</b>. This operation of removing the root and fixing the heap is also called <b>extract-max</b>.
All right, I know how to delete and insert... but how can I create a heap?
At the very beginning we could say that it is enough to add element one by one using the insert operation to get a Heap.
Unfortunately such an operation, although correct, is a bit slow and its time complexity will be O(n log(n)). This is quite a lot. Slightly different method will reduce the time complexity to O(n). Unfortunately I have not yet described this method in this article, although I may update this article later. In short, it's about building a Binary Tree by inserting elements into the array one by one, without worrying about the insertion order. A heapify operation is then performed which fixes the heap.
Nevertheless, this worse method at this stage we do not even have to learn, as it uses the well-known operation: insert. Let me describe this way of creating a heap:
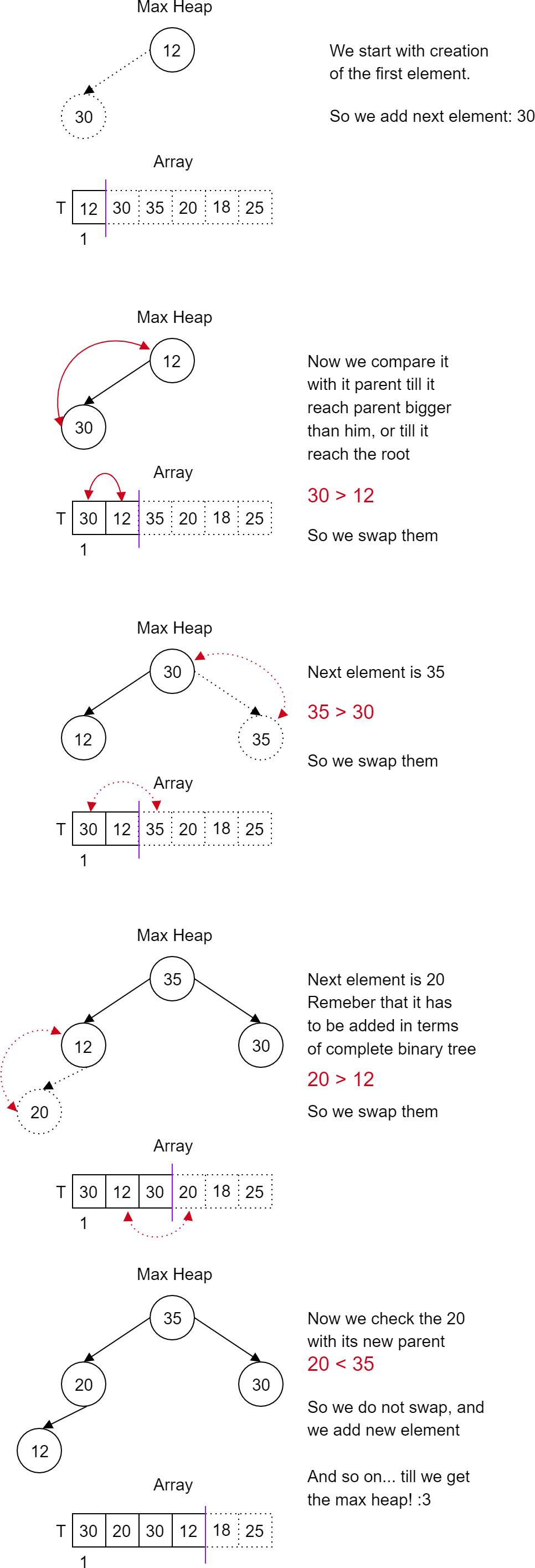
Heap sort is easy!
Heap sort is nothing more than a combination of the two operations that we have just come to know. From this data, we create a heap and then remove its root, which we then hold in the place that we have released. We no longer treat this element as part of the heap. We repeat the operations until we remove the whole heap. We will have a sorted array.

If we would continue we would get:
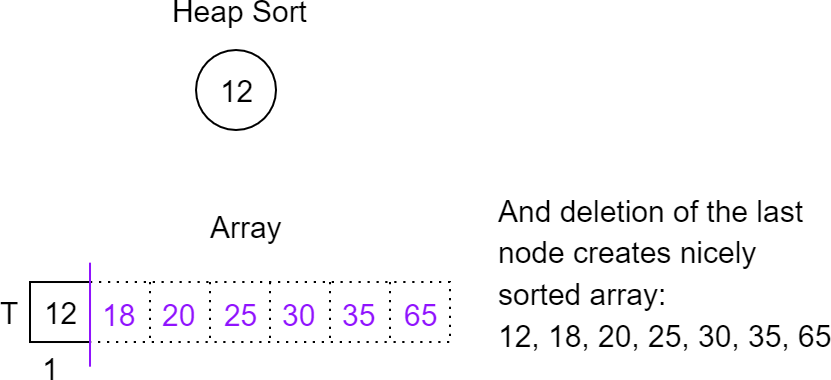
References
Bari, A., 2019. 2.6.3 Heap - Heap Sort - Heapify - Priority Queues. [video] Available at: https://www.youtube.com/watch?v=HqPJF2L5h9U [Accessed 22 December 2020].
En.wikipedia.org. 2020. Heap (Data Structure). [online] Available at: https://en.wikipedia.org/wiki/Heap_(data_structure) [Accessed 22 December 2020].